Array Data Structure

Imagine you have a list of things you want to keep track of, like the scores from your last five game rounds or the names of your friends. How would you store them neatly? An array is one of the simplest and most common ways computers do this. Think of it like a row of numbered boxes, where each box holds one item, and all items are of the same kind (like all numbers or all names). This article will introduce you to the basic idea of arrays, why they are useful, and how they work.

What is an Array?

An array is a fundamental data structure used to efficiently store and manage a collection of elements by using a continuous block of computer memory. This memory is divided into a series of sequential compartments, or slots and each slot can store a single item of information. The items stored within the array can be accessed or modified instantly by using their unique identifiers, known as indices or slot numbers. Here are the key things to know about arrays:

• Same Type: All items (or elements) stored in an array must be of the same data type. For example, an array can hold only numbers (like integers or decimals) or only text (like strings), but not a mix of both in most traditional programming languages.
• Contiguous Memory: The elements of an array are stored right next to each other in the computer’s memory. Imagine a row of connected lockers; if you know the position of where the first locker is, you automatically know where the second, third, and subsequent lockers are.
• Index: Each element in the array has a specific position number, called an index. This index helps us find and access individual elements quickly. Importantly, in most programming languages, indexing starts from 0. So, the first element is at index 0, the second at index 1, and so on.
• Fixed Size (Usually): Traditional arrays have a fixed size, meaning you decide how many elements the array can hold when you create it, and this size doesn’t change afterward. If you need 10 boxes, you get exactly 10.

How Arrays Work (Indexing)

The power of arrays comes from their indexing system. Because all elements are of the same type and stored contiguously, the computer can quickly calculate the exact memory location of any element using its index. Below is how the structure of an array looks like:

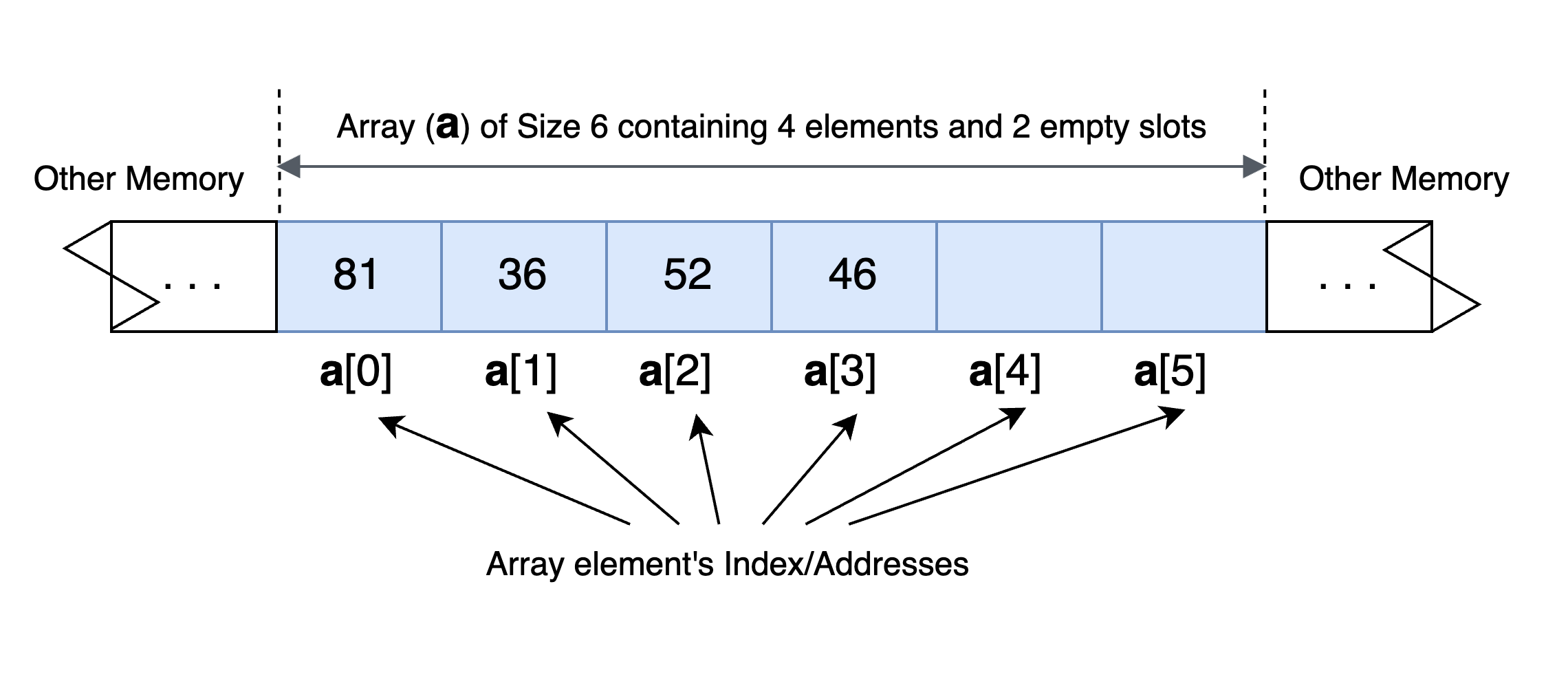
A continuous section of memory space (the area highlighted in blue) is allocated for an Array a. This continuous memory space is further divided into 6 slots where each slot can store an element inside it. Here, the allocated size of the array is 6 (Since the memory is allocated to store a maximum of 6 items). However the actual size of all elements stored in the array is 4, since only the first 4 locations are used for storage.

Let’s say you have an array called scores storing 5 numbers: [95, 80, 100, 75, 90].

• To get the first score, you’d use index 0: scores[0] gives you 95.
• To get the third score, you’d use index 2: scores[2] gives you 100.
• To get the last score (the 5th one), you’d use index 4: scores[4] gives you 90.

This direct access using an index is very fast. In technical terms, accessing an element by its index takes constant time, often written as O(1). This means it takes roughly the same amount of time to access an element, regardless of whether it’s the first, middle, or last element, or how large the array is.

Example situations when an Array Necessary

Any program running on a computer requires storing and accessing of data temporarily. For example, if we write a program to add two numbers, we need to take input the two numbers to add and store them temporarily before adding them and displaying the result.

If the operation we need to do is simple and requires only a few variables, we can store the values in separate variables and perform the operation. For example, if we wish to add two numbers, we can initialize two numbers a and b and create a formula a+b to add the numbers.

But what if we need to add 10 numbers? sure we can initialize 10 variables with names as a1, a2, a3 .. to a10, store all numbers in those variables and add them up using the expression result = a1 + a2 + a3 + ... a10. But what if the number of numbers to add change dynamically? or if the number of numbers to add is very large? This is where an array is really useful.

We can initialize an array to store any number of items we desire and then we can iterate / go through each slot in the array and access the item. For example, if we wish to store 100 items, we can initialize an array like items[100] and start filling each item starting from index 0. So we fill items[0] first, items[1] next and finally items[99]. After filling all the items, we can go through each item and perform required operation like addition, finding the maximum element etc.

Declaring an Array and Accessing Stored Elements

Below are code examples in various programming languages that demonstrate how to create and initialize an array, as well as how to access and modify individual elements within the array.

#include <stdio.h>

int main() {
    // Declare and initialize an integer array
    int numbers[] = {1, 2, 3, 4, 5};

    // Access individual elements by index
    printf("Element at index 2: %d\n", numbers[2]);
    // Element at index 2 is 3

    // Update an element by index
    numbers[2] = 10;

    // Print the updated element
    printf("Updated element at index 2: %d\n", numbers[2]);
    // After the update, element at index 2 is 10

    return 0;
}

# Declare and initialize a list (Python's version of an array)
numbers = [1, 2, 3, 4, 5]

# Access individual elements by index
print("Element at index 2:", numbers[2])
# Element at index 2 is 3

# Update an element by index
numbers[2] = 10

# Print the updated element
print("Updated element at index 2:", numbers[2])
# After the update, element at index 2 is 10

// Declare and initialize an array
let numbers = [1, 2, 3, 4, 5];

// Access individual elements by index
console.log("Element at index 2:", numbers[2]);
// Element at index 2 is 3

// Update an element by index
numbers[2] = 10;

// Print the updated element
console.log("Updated element at index 2:", numbers[2]);
// After the update, element at index 2 is 10

public class ArrayExample {
    public static void main(String[] args) {
        // Declare and initialize an integer array
        int[] numbers = {1, 2, 3, 4, 5};

        // Access individual elements by index
        System.out.println("Element at index 2: " + numbers[2]);
        // Element at index 2 is 3

        // Update an element by index
        numbers[2] = 10;

        // Print the updated element
        System.out.println("Updated element at index 2: " + numbers[2]);
        // After the update, element at index 2 is 10
    }
}

Basic Operations on an Array Data Structure

Following are some of the fundamental operations which can be performed on an Array (Click on the title of each operation to learn more about it):

• Access/Update: This operation involves retrieving or modifying the value of an element at a specific index in the array. It is typically a constant time O(1) operation, as arrays provide direct access to elements using their indices.
• Traversal/Iteration: Traversal/Iteration refers to the process of visiting each element in the array sequentially. This operation is commonly used to perform actions on all elements or to find specific elements based on certain conditions. Traversal usually has a time complexity of O(n), where n is the number of elements in the array.
• Insertion: Insertion is the process of adding a new element to the array. This can be done at the beginning, end, or at a specific position within the array. The time complexity varies depending on the insertion position and whether the array needs to be resized.
• Removal/Deletion: This operation involves removing an element from the array. Like insertion, deletion can be performed at the beginning, end, or at a specific position. The time complexity also varies based on the deletion position and whether subsequent elements need to be shifted.
• Search For an Element: Searching is the process of finding a specific element or set of elements in the array that match certain criteria. Linear search, with O(n) time complexity, is commonly used for unsorted arrays, while binary search, with O(log n) time complexity, can be used for sorted arrays.

Basic Problems on Array Data Structure

Below are some of the problems involving Arrays (Click on the title of each problem to learn more about it):

• Create and Fill Array: This involves initializing an array with a specific size and populating it with elements with inputs from command line.
• Linear Search: This is a simple search algorithm that checks each element of the array sequentially until a match is found or the entire array has been searched. It’s straightforward but can be inefficient for large arrays.
• Sum Elements: This problem requires adding up all the elements in an array to calculate their total sum. It’s a common operation used in various applications, from basic statistics to more complex algorithms.
• Finding Maximum and Minimum: This involves traversing the array to find the largest and smallest elements. It’s useful for understanding the range of values in a dataset and is often a building block for more complex algorithms.
• Reverse an Array: This operation involves flipping the order of elements in an array, so the first element becomes the last, the second becomes the second-to-last, and so on. It’s a common operation that can be achieved through various methods.
• Rotate an Array: This involves shifting all elements of an array by a certain number of positions, either to the left or right. Elements that “fall off” one end of the array are reinserted at the other end. It’s useful in various applications, including image processing and data manipulation.
• Sort an Array of 0s and 1s: This is a specific sorting problem where an array contains only two types of elements (0s and 1s). The goal is to arrange the array so that all 0s come before all 1s. It’s a simplified version of sorting that can be solved more efficiently than general sorting algorithms.

Advanced Array Concepts

• Multi-Dimensional Arrays: Multi-dimensional arrays are data structures that store elements in a grid-like format with two or more dimensions. They can be thought of as “arrays of arrays.” The most common type is a two-dimensional array, which resembles a table with rows and columns. For example, a 3x3 grid for a tic-tac-toe game could be represented as a multi-dimensional array. These arrays are useful for representing complex data relationships, such as matrices in mathematics, pixel data in images, or game boards. They allow for efficient organization and access of data that has a natural grid-like structure.
• Dynamic Arrays: Dynamic arrays are a type of array that can change size during program execution. Unlike static arrays, which have a fixed size determined during creation, dynamic arrays can grow or shrink as needed. This flexibility makes them particularly useful when the amount of data to be stored is not known in advance. Dynamic arrays typically start with an initial capacity and automatically resize when more space is needed, often by creating a new, larger array and copying the existing elements. Many programming languages provide dynamic array implementations, such as ArrayList in Java or vector in C++.