A binary tree is a type of tree data structure which stores collection of items in a hierarchical format. Unlike all the other data structures we have seen so far like arrays, linked lists, stacks etc which are linear, binary trees are two dimensional. Each item is stored in a node which can point out to a maximum of two other child nodes. Each child node can in turn store another item and can have upto two more child nodes.
Anatomy of a Binary Tree
A binary tree is composed of multiple nodes. Each node can store data of any item and can also store links/references to a maximum of two child nodes. The node from which we start accessing all nodes is termed as the root node of a binary tree. Below is how a binary tree looks like:
In the binary tree illustrated above, the node which stores value A is the root node. This is the node from which we generally start traversing other nodes in the tree. The root node A has a connection to another child node B towards it’s left. So node B is called as the left node of node A. Similarly the root node A has a connection to another child node C towards its right. So node C is called as the right child node of node B.
The node B has link to a right child node D and another link to left child node E. But if we look at the node C, it has link to only left child node F. Node C doesn’t link or point to any right child node. Any node in a binary tree which does not contain left and right children is known as a leaf node. In the example above, nodes D, E, F do not have links to left or right childs and so they are called as leaf nodes.
Also, Nodes B and C, which are not root nodes or leaf nodes are called as internal nodes or branch nodes.
Each node in a binary tree should have maximum of two child nodes (left and right) and each node should have only one parent. Below are two example trees which are not binary trees:
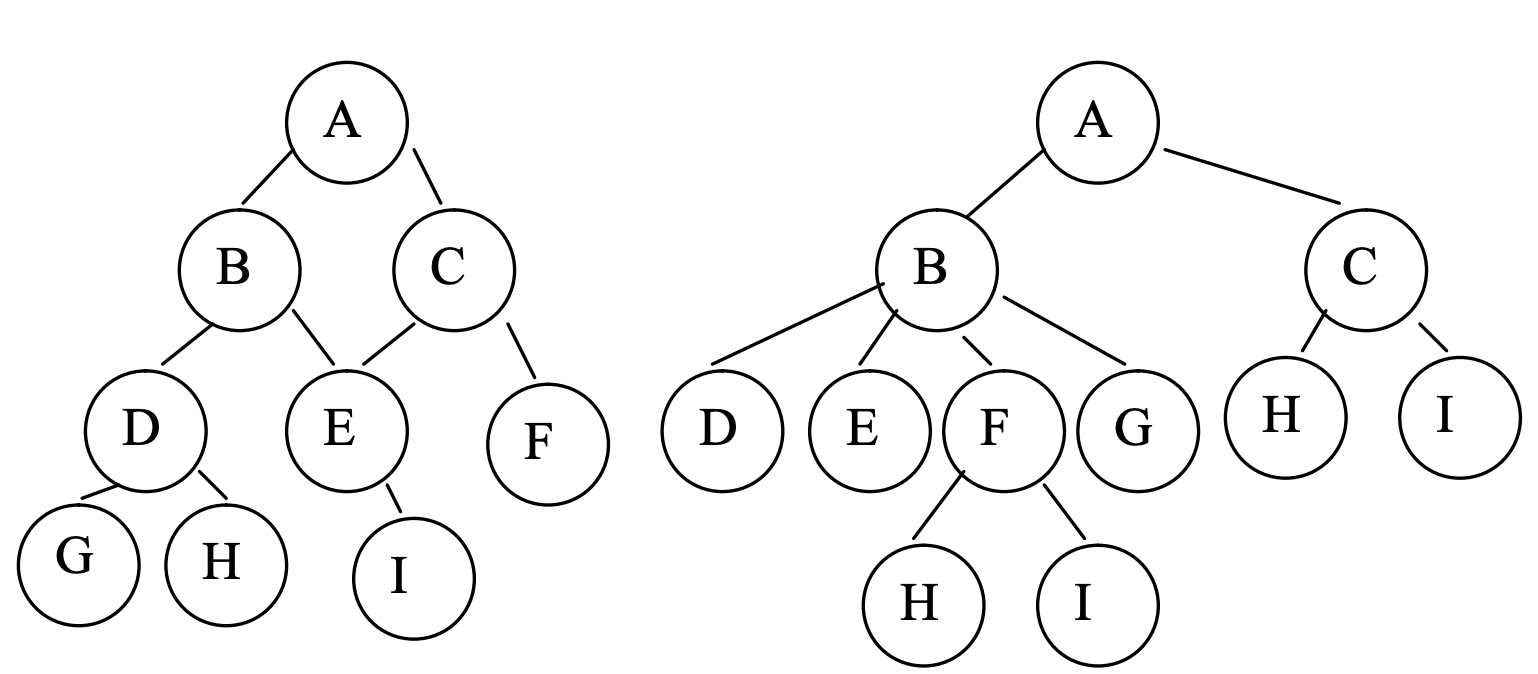
The first tree is not a binary tree because node E has two parents. In a binary tree there will be exactly one parent for each node, except for the root node which does not have any parent node. The second tree is not a binary tree because node B has more that two children.
Other Properties & Terminologies
Here are some of the other terminologies associated with Binary Trees and the nodes which are composed to make the tree:
Depth of any node in a Binary Tree
The depth of any node in a binary tree is the number of links between the node and the root node. For example, between the left child node of the root node and root node, there is only one link. So the depth of the left child node is 1. For root node, there are no links with itself, so it’s depth is 0. Below is an example binary tree with the depths marked for each node.
Between node C and root node A, there is one link. So the depth of node C is 1. Similarly between node F and root node A, there are 2 links. So the depth of node F is 2.
Height of any node in a Binary Tree
The height of node in a binary tree is the maximum number of links present between the node and any leaf node connected to it. Below is an example binary tree with heights marked for each node.
The height of the root node will be the maximum number of links between the root node and any child node connected to it. In the above tree, node G is the farthest leaf node and there are 3 links between node G and root node A. So the height of root node A is 3. Similarly for node B, the farthest leaf node connected to it are nodes D or E and there is only 1 link between them. So the height of node B is 1.
Also, height of a binary tree is the height of the root node of the binary tree. In the above example, the root node is A and it’s height is 3. So height of that binary tree is 3