Memoization is an optimization technique used to speed up computer programs by storing/caching results of expensive computations and by re-using the stored (cached) results in case if we have to do perform the same computation again.
Why Use Memoization?
In the previous article, we looked at recursion technique discussed an example recursive function for finding factorial of a number. Although the factorial recursive function looks really neat and simple, most of the recursive functions have to make multiple computations which are already computed earlier and these redundant computations results in doing more processing than required. This can be rectified by caching results of any expensive computation and re-using the cached results, which is termed as memoization.
Example of an Inefficient Recursive Function
Consider a recursive function for finding nth digit of a fibonacci series. (A fibonacci series is a series where the next number in a series is equal to the sum of last two numbers in the series: 1, 1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 and so on. This series can be generalized as fibonacci(n) = fibonacci(n-2) + fibonacci(n-1).
From the definition it’s pretty straight forward to come up with the below recursive function:
fun fibonacci(n):
if n == 0 or n == 1: # Base Case
return 1
else:
return fibonacci(n-2) + fibonacci(n-1)
Below are how all the recursive calls look like:
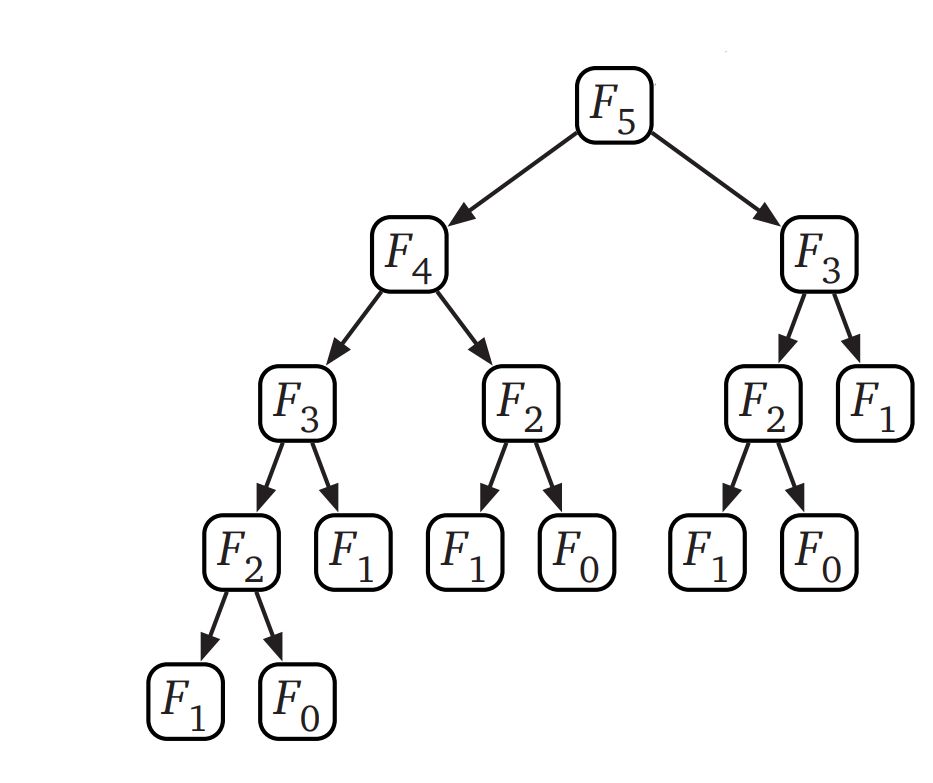
Let’s use the short form for fibonacci function as F
F(5) calls F(4) and F(3)
F(4) calls F(3) and F(2)
F(2) calls F(1) and F(0)
Both fiboncci(1) and fibonacci(0) are base cases and we know that the value is 1, so the recursion stops here.
If you notice the recursion tree carefully, fibonacci(3) is computed twice: one from fibonacci(5) and the other from fibonacci(4). Similarly F(2) is computed twice. To prevent these redundant computations, we can memoize (cache) the results of every recursive call and re-use them whenever we have to do the same computation.
Memoizing Fibonacci Recursive Function
This is how the function looks after memoization:
# Initially memoized (cached) results are empty
memoized_list = [null, null, null ... ]
fun fibonacci(n):
if n == 0 or n == 1: # Base Case
return 1
else:
if memoized_list[n] != null:
return memoized_list[n]
else:
memoized_list[n] = fibonacci(n-2) + fibonacci(n-1)
return memoized_list[n]
Initially, the list of cached results is empty, null indicates that the computation for that index is not done yet. For every recursive call to the function fibonacci, we check if the result for n is already computed and stored in the memoized_list, if it is stored, we directly return the stored result. Otherwise, we compute the result, store the result in memoized_list and then return the result.