Binary trees are a natural choice in solving problems which requires data to be ordered in a two dimensional manner. In this article we will go through some of the use cases which can be efficiently solved using Binary trees.
Efficient Data Organization
In large data sets and databases, efficiently checking if a particular element is present and retrieving it quick is very important. Unordered linear data structures like arrays and linked lists take O(N) time to check if a particular element is present and retrieve it. Which is slow.
We can utilize the structure of binary trees and split data into two subsets based on a rule. For example, given a list of numbers between 0 and 100, we can store all numbers less than 50 under the left subtree and all numbers more than 50 under the right subtree. Now if we wish to check if number 60 is present, we can skip checking all numbers under left subtree as all nodes under it are guaranteed to be less than 50. We only look in the nodes under right subtree using similar logic. This kind of tree is known as binary search tree and is very useful to quickly search and retrieve data. Below is example of a binary search tree:
Expression representation and evaluation
Binary trees can be used to represent and evaluate complex nested arithmetic expressions. Each node contains an operand or operator. For instance, an expression like (3 * (4 + 5)) is represented as a binary tree, where the root node is ‘*’, and its left child is ‘3’, and the right child is ‘+’. The node corresponding to ‘+’ contains node ‘4’ as the left child and node ‘5’ as the right child. This structure allows recursive evaluation by computing the left and right subtrees recursively, ultimately evaluating the entire expression. Below is the expression tree for the expression (3 * (4 + 5)).
Reference Tree for Huffman Encoding
Huffman encoding utilizes binary trees to achieve efficient data compression. By constructing a Huffman tree based on character frequency, each character gets encoded with a unique binary sequence represented by the direction of tree traversal. 1 means we need to traverse to right child and 0 means we need to traverse the left child. For example if the code is 101, we need to traverse the right node of root, then the left node, then it’s right node and we reach the character for which the encoding is 101. More frequent characters have shorter codes, reducing the overall size of the encoded data. Below is an example Huffman tree.
Character A can be reached by going left twice from the root node, so it can be encoded as 00. Similarly character C can be reached by going right child and then to left child, so it can be encoded as 10.
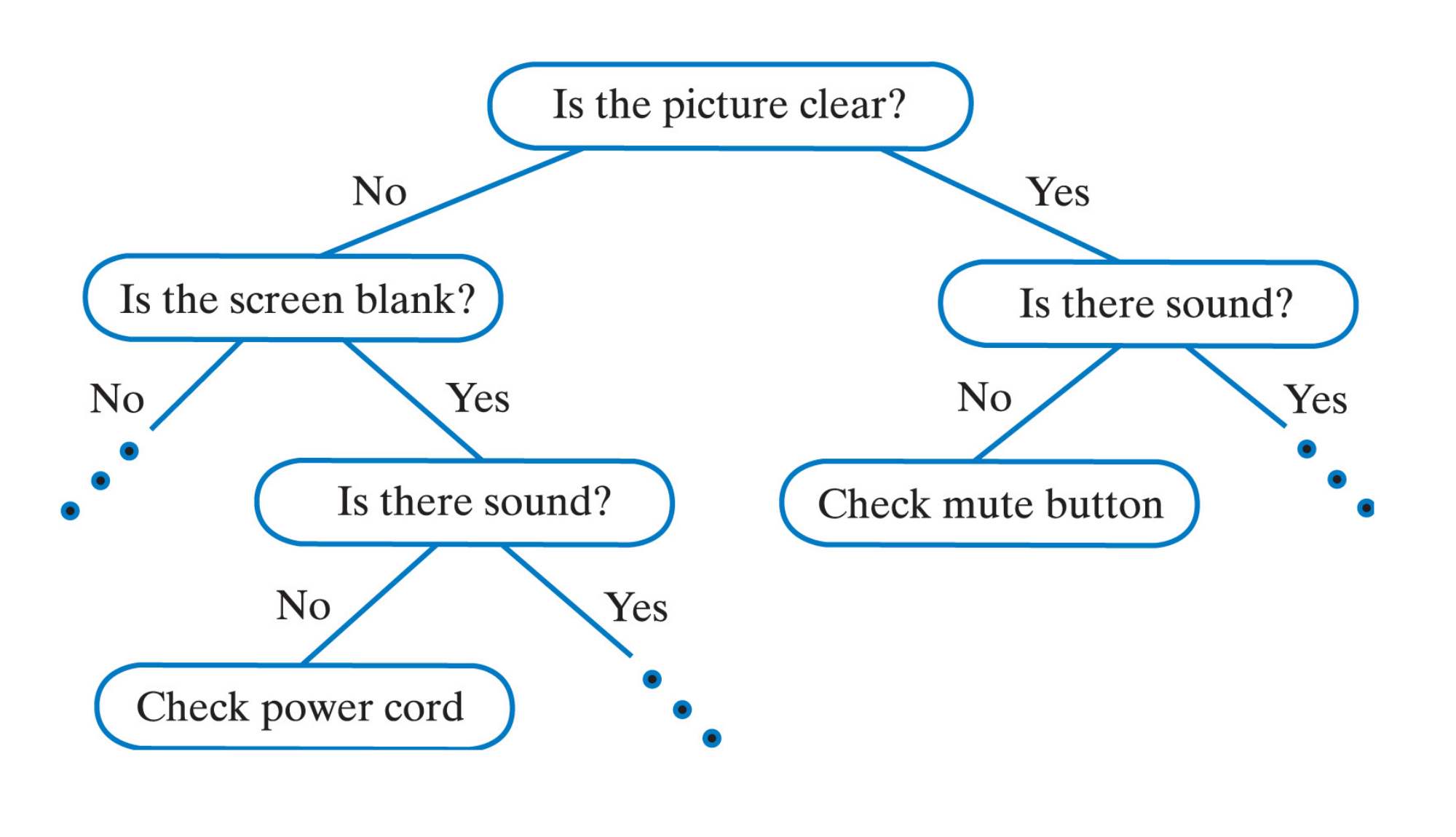
Decision Trees
Binary trees can model decision-making processes by posing yes/no questions at each node. If the answer is no, one can traverse to the left child node and continue with questions. Similarly if the answer is yes, right node can be traversed recursively. The leaf nodes store what action to take. In artificial intelligence or expert systems, decision trees can be used to aid in the process of making choices or reaching conclusions. For instance, in a diagnostic system for medical conditions, a decision tree can ask questions about symptoms, and zero on potential diagnoses based on the patient’s responses. Below is an example binary decision tree.